Téma: Vyvození povrchu jehlanu
Ročník: 9
Pomůcky: mazací tabulka, mazací fix a kousek toaleťáku na mazání, to celé pro každou skupinu 4 žáků, drátěný model jehlanu
Princip: Chci se třídou odvodit výpočet pro povrch jehlanu. Rozdělím děti do skupin po cca 4 (klidně dle vlastní preferenci) a každé skupině dám mazací tabulku, fix a kousek toaleťáku na mazání. První úkol je jasný - napište na tabulku jméno týmu a máte na to 20 sekund. Tím upoutám jejich pozornost, zklidním je ve skupinách. Děti tabulky zvedají, já na tabuli zapíšu týmy.
Mezitím si na tabuli načrtnu jehlan, vedle napíšu, že jde o pravidelný čtyřboký jehlan, podstava měří (například) 8 cm a výška hranolu je 10 cm. Do tohoto obrázku během každého kola vyznačím délku nějaké úsečky a dám dětem pár vteřin na výpočet. Na vyzvání skupiny zvednou tabulku. Kdo zvedne tabulku se správným výsledkem, má bod.
Výsledky píšu na tabuli, a nechávám pro pozdější použití. Takto děti samy přijdou na to, jak se vlastně ten povrch jehlanu počítá a většinou během hodiny stihneme vypočítat i objem (pokud už znají).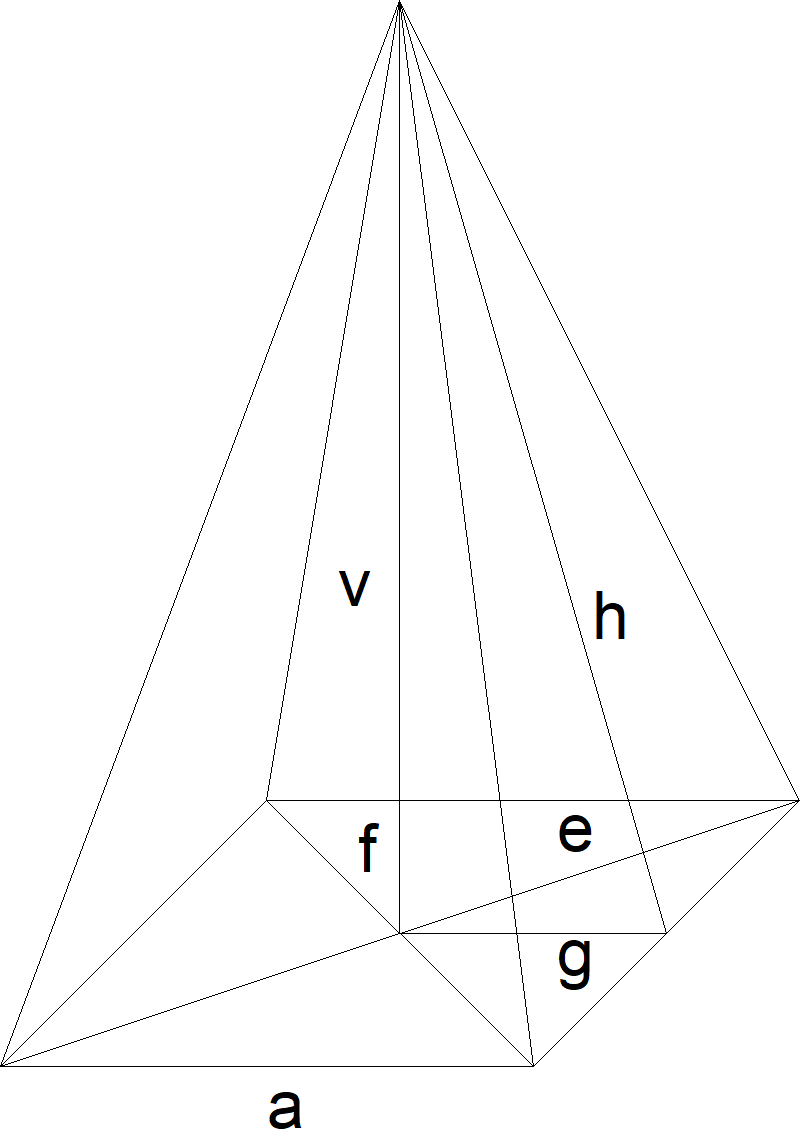
Úkoly za sebou:
1) Úhlopříčka podstavy e =
(čas cca minuta)
2) Druhá úhlopříčka podstavy f =
(čas 10 sekund. Ano, je to stejné, a je zábavné sledovat, jak je nejprve vyděsí ten časový limit a pak jak se rozzáří, když pochopí, že je to stejné jako jednička :-) Vnáší to legraci do hry a navíc se najdou i děti, které to potřebují připomenout).
3) Úsečka spojující střed podstavy a střed boční hrany g =
4) Úsečka spojující střed spodní hrany a vrchol jehlanu h =
5) Obsah podstavy Sp =
6) Obsah boční strany Stroj =
7) Obsah pláště Spl =
8) Povrch celého jehlanu S =
A je to. Ve skupině to děti většinou vymyslí samy a takto si uvědomí, že vlastně všechno znají, že tu není nic, co bych je měla učit. Ty skupiny, které to nevymyslí, tak jsou schopny i po přijímačkách udržet pozornost ty dvě minuty, kdy si jednotlivé kroky rozebíráme a říkáme si, proč to je tolik, kolik to je. A pak se na to navazuje dalším krokem, kdy mají všechny výsledky na tabuli, tak ani skupiny nevstupují do dalšího úkolu s nějakým handicapem z neznalosti, vždy mají možnost udělat další krok. Tím, že se střídají obtížnější kroky (třeba bod 4, bod 6) s jednoduššími (bod 5, bod 7), tak se chytají aspoň někde a to je pro ně motivační.
Podle času můžeme ještě zařadit další kroky:
9) Objem jehlanu
10) Nakreslím místo jehlanu kužel se stejnými rozměry (poloměr podstavy, výška) a vypočítáme jeho objem.
Na závěr krátce zhodnotíme, případně necháme děti, aby si vyfotily tabuli, kde mají postup viditelný (a mají v něm emoce, takže se to i snáze zapamatuje, než strohý zápis do sešitu). Oficiální zápis případně necháme na další hodinu.
